【電験二種過去問解説：電力・管理<H16 問4改>】支持物建て替え前後の電線の弛度と水平張力

問題
解答のポイント
解答

問題

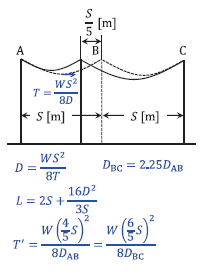
　図の破線のように径間距離が \(S\) [m] で等しく、支持物に高低差がない直線の配電線路がある。中央の支持物を、図の実線のように支持点 A 方向に \(\displaystyle\frac{S}{5}\) [m] の位置に建て替えた場合、支持点 A , B 間のたるみと支持点 A における水平張力は、それぞれ中央の支持物を建て替える前の何倍になるか。ただし、中央の支持物を建て替える前の支持点 A , B 間と支持点 B , C 間のたるみは同じで、支持点 A , C 間の電線の実長は電線の建て替え前後で変わらないものとし、また、中央の支持物の建て替え後の支持点 A と支持点 C における水平張力の大きさは等しいものとする。

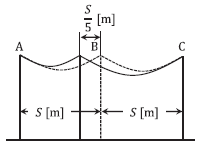
解答のポイント

電線の弛度

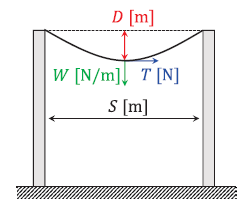
電線のたるみの大きさ \(D\) [m]

　　\(D = \displaystyle\frac{WS^2}{8T}\)　(覚える公式)

電線の実長 \(L\) [m]

　　\(L = S + \displaystyle\frac{8D^2}{3S}\)　(覚える公式)

解答

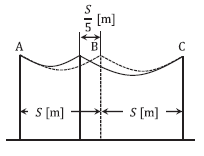
建て替え前の電線の張力 \(T\) [N] 及び電線の実長 \(L\) [m] は、

　　\(D = \displaystyle\frac{WS^2}{8T}\)

　　\(T = \displaystyle\frac{WS^2}{8D}\)

　　\(L = 2\left(S + \displaystyle\frac{8D^2}{3S}\right)\)

　　　 \(= 2S + \displaystyle\frac{16D^2}{3S}\)

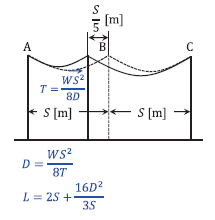
建て替え後の電線の張力 \(T’\) [N] は、

　　\(T’ = \displaystyle\frac{W\left(\displaystyle\frac{4}{5}S\right)^2}{8D_{AB}} = \displaystyle\frac{W\left(\displaystyle\frac{6}{5}S\right)^2}{8D_{BC}}\)

であるから、\(D_{AB}\) と \(D_{BC}\) の関係は、

　　\(\displaystyle\frac{4^2}{D_{AB}} = \displaystyle\frac{6^2}{D_{BC}}\)

　　 \(D_{BC} = \displaystyle\frac{36}{16}D_{AB}\)

　　　　　\(= 2.25D_{AB}\)

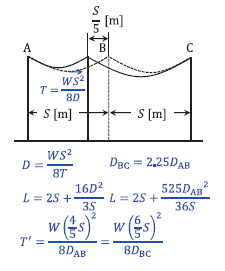
建て替え後の電線の実長 \(L\) [m] は、

\(L = \displaystyle\frac{4}{5}S + \displaystyle\frac{8{D_{AB}}^2}{3\cdot\displaystyle\frac{4}{5}S} = \displaystyle\frac{6}{5}S + \displaystyle\frac{8{D_{BC}}^2}{3\cdot\displaystyle\frac{6}{5}S}\)

　\(= 2S + \displaystyle\frac{40{D_{AB}}^2}{12S} + \displaystyle\frac{40{D_{BC}}^2}{18S}\)

　\(= 2S + \displaystyle\frac{10{D_{AB}}^2}{3S} + \displaystyle\frac{20(2.25D_{AB})^2}{9S}\)

　\(= 2S + \displaystyle\frac{10{D_{AB}}^2}{3S} + \displaystyle\frac{101.25{D_{AB}}^2}{9S}\)

　\(= 2S + \displaystyle\frac{525{D_{AB}}^2}{36S}\)

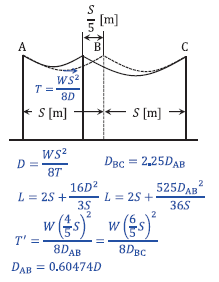
建て替え前後の電線の実長 \(L\) [m] が等しいことから、

\(2S + \displaystyle\frac{16D^2}{3S} = 2S + \displaystyle\frac{525{D_{AB}}^2}{36S}\)

　　　\(\displaystyle\frac{16D^2}{3S} = \displaystyle\frac{525{D_{AB}}^2}{36S}\)

　　　　\(16D^2 = \displaystyle\frac{525{D_{AB}}^2}{12}\)

　　　　\({{D_{AB}}^2} = \displaystyle\frac{16 × 12}{525}D^2\)

　　　　\(D_{AB} = \sqrt{\displaystyle\frac{16 × 12}{525}}D\)

　　　　　　\(\unicode{x2252}\) \(0.60474D\)　→　\(0.605D\)

以上から、建て替え前後の張力の比は、

　　\(\displaystyle\frac{T’}{T} = \displaystyle\frac{\displaystyle\frac{W\left(\displaystyle\frac{4}{5}S\right)^2}{8D_{AB}}}{\displaystyle\frac{WS^2}{8D}} = \displaystyle\frac{\displaystyle\frac{\left(\displaystyle\frac{4}{5}\right)^2}{D_{AB}}}{\displaystyle\frac{1}{D}}\)

　　　　\(=\displaystyle\frac{16D}{25D_{AB}}\)

　　　　\(=\displaystyle\frac{16D}{25 × 0.60474D}\)

　　　　\(\unicode{x2252}\) \(1.06\)