【電験二種過去問解説：電力・管理<R3 問4>】三相3線式高圧配電線への分散型電源の系統連系

問題
解答のポイント
解答

問題

　分散型電源の系統連系に関して、次の問に答えよ。
　図に示す \(6.6\) [kV] 三相3線式高圧配電線の末端に、分散型電源を有する需要家が連系されている。

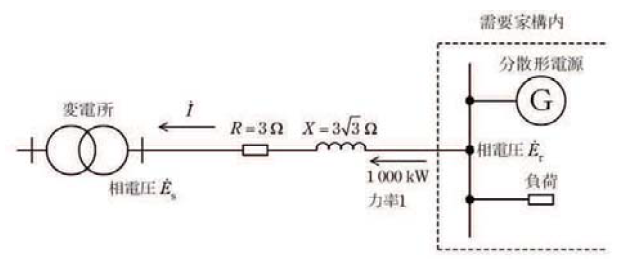
(1)　需要家から配電線へ逆潮流 (力率1) がある場合の、需要家端の相電圧 (1線と中性点間の電圧) \(\dot{E_r}\) と変電所の相電圧 \(\dot{E_s}\) の関係を示すベクトル図及び関係式を \(\dot{E_s}\), \(\dot{E_r}\), \(\dot{I}\), \(R\), \(X\) を用いて描け。ただし、ベクトル図は \(\dot{E_r}\) (位相0) を基準とし、電流 \(\dot{I}\) は図中の矢印の向きを正とする。

(2)　小問(1) のベクトル図から需要家端の線間電圧値を求めよ。ただし、需要家端からの逆潮流は \(1000\) [kW], 力率は1 (分散型電源、負荷設備ともに1) であり、高圧配電線は当該需要家のみの専用線とし、1線当たりの抵抗 \(R\) 及びリアクタンス \(X\) はそれぞれ \(3\) [Ω] 及び \(3\sqrt{3}\) [Ω], 変電所端の線間電圧は \(6.6\) [kV] で一定とする。

解答のポイント

逆潮流が発生した場合のベクトル図

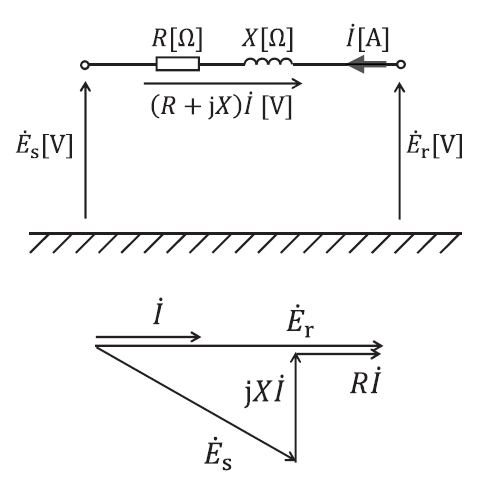
　　\(\dot{E_r} = \dot{E_s} + (R + jX)\dot{I}\)

分散型電源は、無効電力を調整しない (必要がない) ため、基本的には力率は1として考える。

受電端の線間電圧

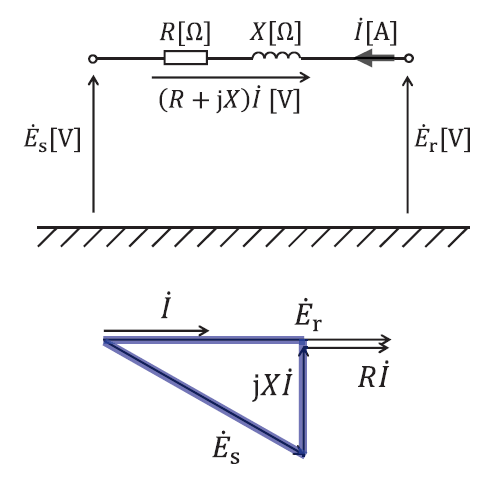
三平方の定理より、

　　\({E_s}^2 = (E_r − RI)^2 + (XI)^2\)

\(P = 3E_rI\) より、

　　\(I = \displaystyle\frac{P}{3E_r}\)

であるから、

　　\({E_s}^2 = \left(E_r − \displaystyle\frac{RP}{3E_r}\right)^2 + \left(\displaystyle\frac{XP}{3E_r}\right)^2\)

　　\({E_s}^2 = {E_r}^2 − 2E_r\cdot\displaystyle\frac{RP}{3E_r} + \left( \displaystyle\frac{RP}{3E_r}\right)^2 + \left(\displaystyle\frac{XP}{3E_r}\right)^2\)

　　　　\(= {E_r}^2 − \displaystyle\frac{2}{3}RP + \displaystyle\frac{R^2P^2}{9{E_r}^2} + \displaystyle\frac{X^2P^2}{9{E_r}^2}\)

　　　　\(= {E_r}^2 − \displaystyle\frac{2}{3}RP + \displaystyle\frac{P^2(R^2 + X^2)}{9{E_r}^2}\)

　\(3{E_s}^2= 3{E_r}^2 − 2RP + \displaystyle\frac{P^2(R^2 + X^2)}{3{E_r}^2}\)

\(V_s = \sqrt{3}E_s\)、\(V_r = \sqrt{3}E_r\) であるから、

　\(3{E_s}^2= 3{E_r}^2 − 2RP + \displaystyle\frac{P^2(R^2 + X^2)}{3{E_r}^2}\)

　　\({V_s}^2= {V_r}^2 − 2RP + \displaystyle\frac{P^2(R^2 + X^2)}{{V_r}^2}\)

　　\({V_r}^2 − 2RP − {V_s}^2 + \displaystyle\frac{P^2(R^2 + X^2)}{{V_r}^2} = 0\)

　　\({V_r}^4 − (2RP + {V_s}^2){V_r}^2 + P^2(R^2 + X^2) = 0\)

\({V_r}^2\) について解くと、

　　\({V_r}^2 = \displaystyle\frac{2RP + {V_s}^2 \pm\sqrt{{(2RP + {V_s}^2)}^2 − 4P^2(R^2 + X^2)}}{2}\)

\(V_r\) を求めると、

　　\(V_r = \sqrt{\displaystyle\frac{2RP + {V_s}^2 \pm\sqrt{{(2RP + {V_s}^2)}^2 − 4P^2(R^2 + X^2)}}{2}}\)

解答

(1)　需要家から配電線へ逆潮流 (力率1) がある場合の、需要家端の相電圧 (1線と中性点間の電圧) \(\dot{E_r}\) と変電所の相電圧 \(\dot{E_s}\) の関係を示すベクトル図及び関係式

ベクトル図は以下の通り。

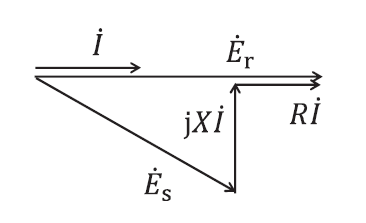
関係式は、

　　\(\dot{E_r} = \dot{E_s} + (R + jX)\dot{I}\)

(2)　需要家端の線間電圧値

ベクトル図に三平方の定理を適用すると、

　　\({E_s}^2 = (E_r − RI)^2 + (XI)^2\)

ここで、\(P = 3E_rI\) より、

　　\(I = \displaystyle\frac{P}{3E_r}\)

であるから、

　　\({E_s}^2 = \left(E_r − \displaystyle\frac{RP}{3E_r}\right)^2 + \left(\displaystyle\frac{XP}{3E_r}\right)^2\)

　　\({E_s}^2 = {E_r}^2 − 2E_r\cdot\displaystyle\frac{RP}{3E_r} + \left( \displaystyle\frac{RP}{3E_r}\right)^2 + \left(\displaystyle\frac{XP}{3E_r}\right)^2\)

　　　　\(= {E_r}^2 − \displaystyle\frac{2}{3}RP + \displaystyle\frac{R^2P^2}{9{E_r}^2} + \displaystyle\frac{X^2P^2}{9{E_r}^2}\)

　　　　\(= {E_r}^2 − \displaystyle\frac{2}{3}RP + \displaystyle\frac{P^2(R^2 + X^2)}{9{E_r}^2}\)

　\(3{E_s}^2= 3{E_r}^2 − 2RP + \displaystyle\frac{P^2(R^2 + X^2)}{3{E_r}^2}\)

\(V_s = \sqrt{3}E_s\)、\(V_r = \sqrt{3}E_r\) であるから、

　\(3{E_s}^2= 3{E_r}^2 − 2RP + \displaystyle\frac{P^2(R^2 + X^2)}{3{E_r}^2}\)

　　\({V_s}^2= {V_r}^2 − 2RP + \displaystyle\frac{P^2(R^2 + X^2)}{{V_r}^2}\)

　　\({V_r}^2 − 2RP − {V_s}^2 + \displaystyle\frac{P^2(R^2 + X^2)}{{V_r}^2} = 0\)

　　\({V_r}^4 − (2RP + {V_s}^2){V_r}^2 + P^2(R^2 + X^2) = 0\)

各値を代入すると、

　　\({V_r}^4 − (2 × 3 × 1000 × 10^3 + 6600^2){V_r}^2 + (1000 × 10^3)^2\{3^2 + (3\sqrt{3})^2\} = 0\)

　　\({V_r}^4 − 49.56 × 10^6{V_r}^2 + 36 × 10^{12} = 0\)

\({V_r}^2\) について解くと、