問題
電線のたるみの曲線式を放物線で近似すると、次の式で表すことができる。
\(Y = \displaystyle\frac{X^2}{2a}\)
ここで、\(Y\) [m]:縦軸方向の変数、\(X\) [m]:横軸方向の変数、\(a\) :係数とする。
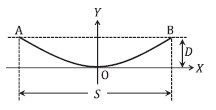
図において、支持点における電線水平張力を \(T\) [N]、電線単位長さ当たりの重量を \(W\) [N/m]、径間の長さを \(S\) [m] とし、たるみの最下点 O を座標軸の原点としたとき、たるみ \(D\) [m] は次式で表されることを証明せよ。ただし、電線各点の張力は、その水平張力と同一とみなすことができ、電線の材質が一様で、径間に比べてたるみが十分に小さいものとする。
\(D = \displaystyle\frac{WS^2}{8T}\)
解答のポイント
電線の弛度
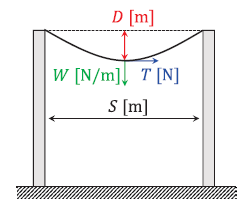
電線のたるみの大きさ \(D\) [m]
\(D = \displaystyle\frac{WS^2}{8T}\) (覚える公式)
電線の実長 \(L\) [m]
\(L = S + \displaystyle\frac{8D^2}{3S}\) (覚える公式)
解答
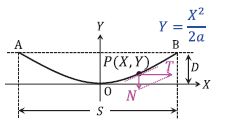
点 \(P (X, Y)\) での傾きは、
\(\displaystyle\frac{dY}{dX} = \displaystyle\frac{X}{a}\)
点 \(P\) での水平張力を \(T\) [N]、垂直張力を \(N\) [N] とすると、
\(\displaystyle\frac{N}{T}\) \(\unicode{x2252}\) \(\displaystyle\frac{WX}{T} = \displaystyle\frac{X}{a}\)
\(a = \displaystyle\frac{T}{W}\)
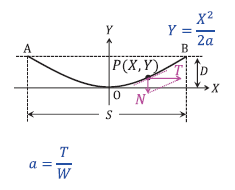
\(Y = \displaystyle\frac{X^2}{2a}\) に \(a = \displaystyle\frac{T}{W}\) を代入すると、
\(Y = \displaystyle\frac{X^2}{2\cdot\displaystyle\frac{T}{W}}\)
\(= \displaystyle\frac{W}{2T}X^2\)
\(X = \displaystyle\frac{S}{2}\) において、\(Y = D\) であるから、
\(D = \displaystyle\frac{W}{2T}\left(\displaystyle\frac{S}{2}\right)^2\)
\(= \displaystyle\frac{WS^2}{8T}\)



![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/44434784.9658043e.44434785.1b56e7db/?me_id=1213310&item_id=21435347&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F1849%2F9784485121849_1_72.jpg%3F_ex%3D240x240&s=240x240&t=picttext)

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/44434784.9658043e.44434785.1b56e7db/?me_id=1213310&item_id=20480019&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F0639%2F9784485100639_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext)

コメント