問題
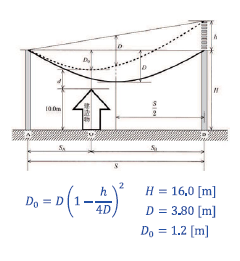
図のように、平たんな地形 A - B 間を経過する電線支持点に高低差のない公称電圧 \(154\) [kV] の架空送電線で、B 側の鉄塔建替え工事のみで電線支持点を嵩上げして、点線で示すように電線線下のどの地点においても、「電気設備技術基準の解釈」で規定される電線との離隔距離を確保し、高さ \(10.0\) [m] の建造物が建築可能となるようにする場合、次の問に答えよ。
ただし、嵩上げ前後の電線張力を変えないものとする。
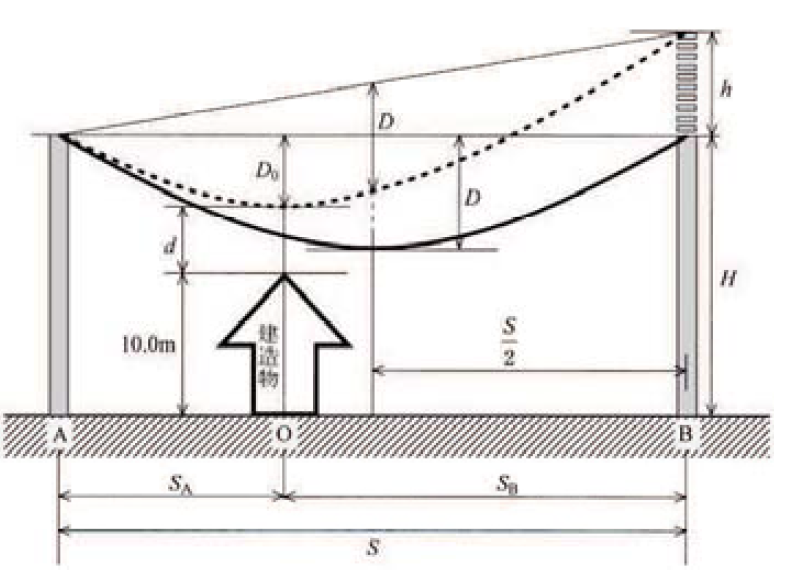
(1) 電線の最低地上高となる地点 O での電線たるみ \(D_0\) を、径間中央たるみ \(D\) と電線支持点の嵩上げ量 \(h\) を用いて表せ。
(2) 嵩上げ前の電線支持点高さ \(H = 16.0\) [m] , 電線水平たるみ \(D = 3.80\) [m] とするとき、 \(154\) [kV] 架空送電線の電線と建造物との離隔距離 \(d\) が、「電気設備技術基準の解釈」で規定される離隔距離 \(d_0 = 4.80\) [m] を確保する最低嵩上げ量 \(h_0\) [m] を求めよ。
解答のポイント
支持物に高低差がある場合の電線の弛度
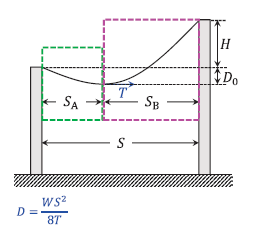
左図より、
\(D_0 = \displaystyle\frac{W(2S_A)^2}{8T}\)
\(D_0 + H = \displaystyle\frac{W(2S_B)^2}{8T}\)
\(S_A + S_B = S\)
これらの関係式より、\(S_A\) と \(S_B\) を消去して求める。
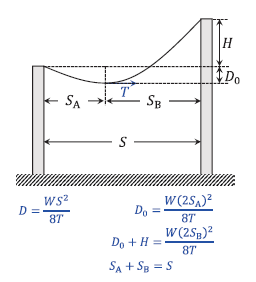
\(H = \displaystyle\frac{W(2S_B)^2}{8T} − \displaystyle\frac{W(2S_A)^2}{8T}\)
\(= \displaystyle\frac{W}{8T}\{(2S_B)^2 − (2S_A)^2\}\)
\(= \displaystyle\frac{W}{2T}({S_B}^2 − {S_A}^2)\)
\(= \displaystyle\frac{W}{2T}(S_B + S_A)(S_B − S_A)\)
\(= \displaystyle\frac{W}{2T}S(S − S_A − S_A)\)
\(= \displaystyle\frac{W}{2T}S(S − 2S_A)\)
\(= 4\displaystyle\frac{WS^2}{8T}\left(1 − \displaystyle\frac{2S_A}{S}\right)\)
\(= 4D\left(1 − \displaystyle\frac{2S_A}{S}\right)\)
\(1 − \displaystyle\frac{2S_A}{S} = \displaystyle\frac{H}{4D}\)
\(\displaystyle\frac{2S_A}{S} = 1 − \displaystyle\frac{H}{4D}\)
\(S_A = \displaystyle\frac{S}{2}\left(1 − \displaystyle\frac{H}{4D}\right)\)
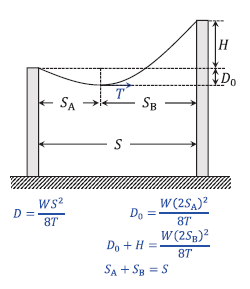
したがって \(D_0\) は、
\(D_0 = \displaystyle\frac{W\left\{2\cdot\displaystyle\frac{S}{2}\left(1 − \displaystyle\frac{H}{4D}\right)\right\}^2}{8T}\)
\(= \displaystyle\frac{W\left\{S\left(1 − \displaystyle\frac{H}{4D}\right)\right\}^2}{8T}\)
\(= \displaystyle\frac{WS^2}{8T}\left(1 − \displaystyle\frac{H}{4D}\right)^2\)
\(= D\left(1 − \displaystyle\frac{H}{4D}\right)^2\)
解答
(1) 電線の最低地上高となる地点 O での電線たるみ \(D_0\)
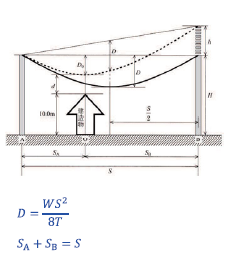
問題図より、
\(D_0 = \displaystyle\frac{W(2S_A)^2}{8T}\)
\(D_0 + h = \displaystyle\frac{W(2S_B)^2}{8T}\)
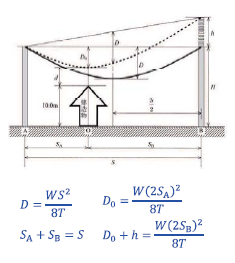
したがって、
\(h = \displaystyle\frac{W(2S_B)^2}{8T} − \displaystyle\frac{W(2S_A)^2}{8T}\)
\(= \displaystyle\frac{W}{8T}\{(2S_B)^2 − (2S_A)^2\}\)
\(= \displaystyle\frac{W}{2T}({S_B}^2 − {S_A}^2)\)
\(= \displaystyle\frac{W}{2T}(S_B + S_A)(S_B − S_A)\)
\(= \displaystyle\frac{W}{2T}S(S − S_A − S_A)\)
\(= \displaystyle\frac{W}{2T}S(S − 2S_A)\)
\(= 4\displaystyle\frac{WS^2}{8T}\left(1 − \displaystyle\frac{2S_A}{S}\right)\)
\(= 4D\left(1 − \displaystyle\frac{2S_A}{S}\right)\)
\(1 − \displaystyle\frac{2S_A}{S} = \displaystyle\frac{h}{4D}\)
\(\displaystyle\frac{2S_A}{S} = 1 − \displaystyle\frac{h}{4D}\)
\(S_A = \displaystyle\frac{S}{2}\left(1 − \displaystyle\frac{h}{4D}\right)\)
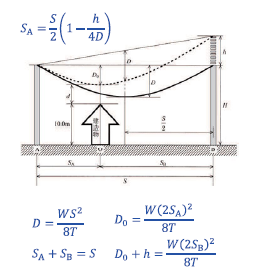
したがって \(D_0\) は、
\(D_0 = \displaystyle\frac{W\left\{2\cdot\displaystyle\frac{S}{2}\left(1 − \displaystyle\frac{h}{4D}\right)\right\}^2}{8T}\)
\(= \displaystyle\frac{W\left\{S\left(1 − \displaystyle\frac{h}{4D}\right)\right\}^2}{8T}\)
\(= \displaystyle\frac{WS^2}{8T}\left(1 − \displaystyle\frac{h}{4D}\right)^2\)
\(= D\left(1 − \displaystyle\frac{h}{4D}\right)^2\)
(2) 離隔距離 \(d_0 = 4.80\) [m] を確保する最低嵩上げ量 \(h_0\) [m]
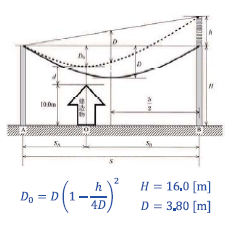
\(d_0 = 4.80\) [m] より、\(D_0\) [m] は、
\(D_0 = H − 10 − d_0\)
\(= 16.0 − 10 − 4.80\)
\(= 1.2\) [m]
(1) 解答式より、
\(D_0 = D\left(1 − \displaystyle\frac{h_0}{4D}\right)^2\)
\(\left(1 − \displaystyle\frac{h_0}{4D}\right)^2 = \displaystyle\frac{D_0}{D}\)
\(1 − \displaystyle\frac{h_0}{4D} = \sqrt{\displaystyle\frac{D_0}{D}}\)
\(\displaystyle\frac{h_0}{4D} = 1 − \sqrt{\displaystyle\frac{D_0}{D}}\)
\(h_0 = 4D\left(1 − \sqrt{\displaystyle\frac{D_0}{D}}\right)\)
\(= 4 × 3.80 × \left(1 − \sqrt{\displaystyle\frac{1.2}{3.80}}\right)\)
\(\unicode{x2252}\) \(6.66\) [m]



![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/44434784.9658043e.44434785.1b56e7db/?me_id=1213310&item_id=21435347&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F1849%2F9784485121849_1_72.jpg%3F_ex%3D240x240&s=240x240&t=picttext)

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/44434784.9658043e.44434785.1b56e7db/?me_id=1213310&item_id=20480019&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F0639%2F9784485100639_1_2.jpg%3F_ex%3D240x240&s=240x240&t=picttext)

コメント